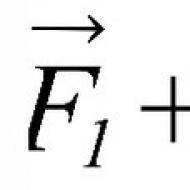
Ускорение движении тела по наклонной плоскости. Движение по наклонной плоскости тела: скорость, трение, время. Задача на определение ускорения при движении по наклонной плоскости тела

Динамика является одним из важных разделов физики, который изучает причины движения тел в пространстве. В данной статье рассмотрим с точки зрения теории одну из типичных задач динамики — движение тела по наклонной плоскости, а также приведем примеры решений некоторых практических проблем.

Основная формула динамики

Прежде чем переходить к изучению физики движения тела по плоскости наклонной, приведем необходимые теоретические сведения для решения этой задачи.

В XVII Исаак Ньютон благодаря практическим наблюдениям за движением макроскопических окружающих тел вывел три закона, носящих в настоящее время его фамилию. На этих законах зиждется вся классическая механика. Нас интересует в данной статье лишь второй закон. Его математический вид приведен ниже:

Формула говорит о том, что действие внешней силы F¯ придаст ускорение a¯ телу массой m. Это простое выражение будем далее использовать для решения задач движения тела по плоскости наклонной.

Отметим, что сила и ускорение — это величины векторные, направленные в одну и ту же сторону. Кроме того, сила — это аддитивная характеристика, то есть в приведенной формуле F¯ можно рассматривать как результирующее воздействие на тело.

Наклонная плоскость и силы, действующие на тело, находящееся на ней

Ключевым моментом, от которого зависит успех решения задач движения тела по плоскости наклонной, является определение действующих на тело сил. Под определением сил понимают знание их модулей и направлений действия.

Ниже дан рисунок, где показано, что тело (автомобиль) находится в покое на наклоненной под углом к горизонту плоскости. Какие силы на него действуют?

Список ниже перечисляет эти силы:

• тяжести;
• реакции опоры;
• трения;
• натяжения нити (если присутствует).

Сила тяжести

В первую очередь это сила тяжести (F g). Она направлена вертикально вниз. Поскольку тело имеет возможность двигаться только вдоль поверхности плоскости, то при решении задач силу тяжести разлагают на две взаимно перпендикулярные составляющие. Одна из составляющих направлена вдоль плоскости, другая — перпендикулярна ей. Только первая из них приводит к появлению у тела ускорения и, по сути, является единственным движущим фактором для рассматриваемого тела. Вторая составляющая обуславливает возникновение силы реакции опоры.

Реакция опоры

Второй действующей на тело силой является реакция опоры (N). Причина ее появления связана с третьим законом Ньютона. Величина N показывает, с какой силой плоскость воздействует на тело. Она направлена вверх перпендикулярно плоскости наклонной. Если бы тело находилось на горизонтальной поверхности, то N равнялась бы его весу. В рассматриваемом же случае N равна лишь второй составляющей, полученной при разложении силы тяжести (см. абзац выше).

Реакция опоры не оказывает прямого воздействия на характер движения тела, поскольку она перпендикулярна плоскости наклона. Тем не менее она обуславливает появление трения между телом и поверхностью плоскости.

Сила трения

Третьей силой, которую следует учитывать при исследовании движения тела по наклонной плоскости, является трение (F f). Физическая природа трения является непростой. Ее появление связано с микроскопическими взаимодействиями соприкасающихся тел, имеющих неоднородные поверхности контакта. Выделяют три вида этой силы:

• покоя;
• скольжения;
• качения.

Трение покоя и скольжения описываются одной и той же формулой:

где µ — это безразмерный коэффициент, значение которого определяется материалами трущихся тел. Так, при трении скольжения дерева о дерево µ = 0,4, а льда о лед — 0,03. Коэффициент для трения покоя всегда больше такового для скольжения.

Трение качения описывается по отличной от предыдущей формуле. Она имеет вид:

Здесь r — радиус колеса, f — коэффициент, имеющий размерность обратной длины. Эта сила трения, как правило, намного меньше предыдущих. Заметим, что на ее значение влияет радиус колеса.

Сила F f , какого бы типа она ни была, всегда направлена против движения тела, то есть F f стремится остановить тело.

Натяжение нити

При решении задач движения тела по наклонной плоскости эта сила не всегда присутствует. Ее появление определяется тем, что находящееся на наклонной плоскости тело связано с помощью нерастяжимой нити с другим телом. Часто второе тело свисает на нити через блок за пределами плоскости.

На находящийся на плоскости предмет, сила натяжение нити воздействует либо ускоряя его, либо замедляя. Все зависит от модулей сил, действующих в физической системе.

Появление этой силы в задаче значительно усложняет процесс решения, поскольку приходится рассматривать одновременно движение двух тел (на плоскости и свисающего).

Задача на определение критического угла

Теперь пришло время применить описанную теорию для решения реальных задач движения по наклонной плоскости тела.

Предположим, что брус из дерева имеет массу 2 кг. Он находится на деревянной плоскости. Следует определить, при каком критическом угле наклона плоскости брус начнет по ней скользить.

Скольжение бруса наступит только тогда, когда суммарная действующая вниз вдоль плоскости сила на него окажется больше нуля. Таким образом, чтобы решить эту задачу, достаточно определить результирующую силу и найти угол, при котором она станет больше нуля. Согласно условию задачи на брус будут вдоль плоскости оказывать действие только две силы:

• составляющая силы тяжести F g1 ;
• трение покоя F f .

Чтобы началось скольжение тела, должно выполняться условие:

Отметим, что если составляющая силы тяжести превысит трение покоя, то она также будет больше силы трения скольжения, то есть начавшееся движение будет продолжаться с постоянным ускорением.

Рисунок ниже показывает направления всех действующих сил.

Обозначим критический угол символом θ. Несложно показать, что силы F g1 и F f будут равны:

F g1 = m × g × sin(θ);

F f = µ × m × g × cos(θ).

Здесь m × g — это вес тела, µ — коэффициент силы трения покоя для пары материалов дерево-дерево. Из соответствующей таблицы коэффициентов можно найти, что он равен 0,7.

Подставляем найденные величины в неравенство, получаем:

m × g × sin(θ) ≥ µ × m × g × cos(θ).

Преобразуя это равенство, приходим к условию движения тела:

tg(θ) ≥ µ =>

θ ≥ arctg(µ).

Мы получили весьма интересный результат. Оказывается, значение критического угла θ не зависит от массы тела на наклонной плоскости, а однозначно определяется коэффициентом трения покоя µ. Подставляя его значение в неравенство, получим величину критического угла:

θ ≥ arctg(0,7) ≈ 35 o .

Задача на определение ускорения при движении по наклонной плоскости тела

Теперь решим несколько иную задачу. Пусть на стеклянной наклонной плоскости находится брус из дерева. Плоскость к горизонту наклонена под углом 45 o . Следует определить, с каким ускорением будет двигаться тело, если его масса равна 1 кг.

Запишем главное уравнение динамики для этого случая. Поскольку сила F g1 будет направлена вдоль движения, а F f против него, то уравнение примет вид:

F g1 — F f = m × a.

Подставляем полученные в предыдущей задаче формулы для сил F g1 и F f , имеем:

m × g × sin(θ) — µ × m × g × cos(θ) = m × a.

Откуда получаем формулу для ускорения:

a = g × (sin(θ) — µ × cos(θ)).

Снова мы получили формулу, в которой нет массы тела. Этот факт означает, что бруски любой массы будут соскальзывать за одно и то же время по наклонной плоскости.

Учитывая, что коэффициент µ для трущихся материалов дерево-стекло равен 0,2, подставим все параметры в равенство, получим ответ:

Таким образом, методика решения задач с наклонной плоскостью заключается в определении результирующей силы, действующей на тело, и в последующем применении второго закона Ньютона.

Физика: движение тела по наклонной плоскости. Примеры решения и задачи — все интересные факты и достижения науки и образования на сайт

Динамика и кинематика - это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

Здесь M и I - и инерции, соответственно, α - угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

S = v 0 *t ± a*t 2 /2

Здесь v 0 - значение начальной скорости тела, S - пройденный за время t путь вдоль прямолинейной траектории. Знак "+" следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак "-". Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

ω = ω 0 ± α*t;

θ = ω 0 *t ± α*t 2 /2

Здесь α и ω - и скорость, соответственно, θ - угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

Здесь r - радиус вращения.

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

Где N - реакция опоры, µ - коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) - µ*m*g*cos(φ) = m*g*(sin(φ) - µ*cos(φ)) = m*a

Здесь φ - это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) - F r = m*a

Где F r - Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F r создает следующий момент:

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45 o . Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) - µ*cos(φ)) = m*a =>

a = g*(sin(φ) - µ*cos(φ)) ≈ 4,162 м/с 2

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30 o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) - F r = m*a;

F r *r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

Подставим это значение во вторую формулу, выразим из нее силу трения F r и заменим полученным выражением ее в первом уравнении, имеем:

F r *r = 1/2*m*r 2 *a/r = >

m*g*sin(φ) - 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Тело, которое соскальзывает вниз по наклонной плоскости . В этом случае на него действуют следующие силы:

Сила тяжести mg, направленная вертикально вниз;

Сила реакции опоры N, направленная перпендикулярно плоскости;

Сила трения скольжения Fтр, направлена противоположно скорости (вверх вдоль наклонной плоскости при соскальзывании тела).

Введем наклонную систему координат, ось OX которой направлена вдоль плоскости вниз. Это удобно, потому что в этом случае придется раскладывать на компоненты только один вектор - вектор силы тяжести mg, а вектора силы трения Fтр и силы реакции опоры N уже направлены вдоль осей. При таком разложении x-компонента силы тяжести равна mg sin(α) и соответствует «тянущей силе», ответственной за ускоренное движение вниз, а y-компонента - mg cos(α) = N уравновешивает силу реакции опоры, поскольку вдоль оси OY движение тела отсутствует.

Сила трения скольжения Fтр = µN пропорциональна силе реакции опоры. Это позволяет получить следующее выражение для силы трения: Fтр = µmg cos(α). Эта сила противонаправлена «тянущей» компоненте силы тяжести. Поэтому для тела, соскальзывающего вниз, получаем выражения суммарной равнодействующей силы и ускорения:

Fx = mg(sin(α) – µ cos(α));

ax = g(sin(α) – µ cos(α)).

ускорение:

скорость равна

v=ax*t=t*g(sin(α) – µ cos(α))

через t=0.2 с

скорость равна

v=0.2*9.8(sin(45)-0.4*cos(45))=0.83 м/с

Силу, с которой тело притягивается к Земле под действием поля тяготения Земли, называют силой тяжести. По закону всемирного тяготения на поверхности Земли (или вблизи этой поверхности) на тело массой m действует сила тяжести

Fт=GMm/R2 (2.28)

где М - масса Земли; R - радиус Земли.

Если на тело действует только сила тяжести, а все другие силы взаимно уравновешены, тело совершает свободное падение. Согласно второму закону Ньютона и формуле (2,28) модуль ускорения свободного падения g находят по формуле

g=Fт/m=GM/R2. (2.29)

Из формулы (2.29) следует, что ускорение свободного падения не зависит от массы m падающего тела, т.е. для всех тел в данном месте Земли оно одинаково. Из формулы (2.29) следует, что Fт = mg. В векторном виде

В § 5 было отмечено, что поскольку Земля не шар, а эллипсоид вращения, ее полярный радиус меньше экваториального. Из формулы (2.28) видно, что по этой причине сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе.

Сила тяжести действует на все тела, находящиеся в поле тяготения Земли, однако не все тела падают на Землю. Это объясняется тем, что движению многих тел препятствуют другие тела, например опоры, нити подвеса и т. п. Тела, ограничивающие движение других тел, называют связями. Под действием силы тяжести связи деформируются и сила реакции деформированной связи по третьему закону Ньютона уравновешивает силу тяжести.

В § 5 отмечалось также, что на ускорение свободного падения влияет вращение Земли. Это влияние объясняется так. Системы отсчета, связанные с поверхностью Земли (кроме двух, связанных с полюсами Земли), не являются, строго говоря, инерциальными системами отсчета - Земля вращается вокруг своей оси, а вместе с ней движутся по окружностям с центростремительным ускорением и такие системы отсчета. Эта неинерциальность систем отсчета проявляется, в частности, в том, что значение ускорения свободного падения оказывается различным в разных местах Земли и зависит от географической широты того места, где находится связанная с Землей система отсчета, относительно которой определяется ускорение свободного падения.

Измерения, проведенные на разных широтах, показали, что числовые значения ускорения свободного падения мало отличаются друг от друга. Поэтому при не очень точных расчетах можно пренебречь неинерциальностью систем отсчета, связанных с поверхностью Земли, а также отличием формы Земли от сферической, и считать, что ускорение свободного падения в любом месте Земли одинаково и равно 9,8 м/с2.

Из закона всемирного тяготения следует, что сила тяжести и вызываемое ею ускорение свободного падения уменьшаются при увеличении расстояния от Земли. На высоте h от поверхности Земли модуль ускорения свободного падения определяют по формуле

Установлено, что на высоте 300 км над поверхностью Земли ускорение свободного падения меньше, чем у поверхности Земли, на 1 м/с2.

Следовательно, вблизи Земли (до высот нескольких километров) сила тяжести практически не изменяется, а потому свободное падение тел вблизи Земли является движением равноускоренным.

Вес тела. Невесомость и перегрузки

Силу, в которой вследствие притяжения к Земле тело действует на свою опору или подвес, называют весом тела. В отличие от силы тяжести, являющейся гравитационной силой, приложенной к телу, вес - это упругая сила, приложенная к опоре или подвесу (т. е. к связи).

Наблюдения показывают, что вес тела Р, определяемый на пружинных весах, равен действующей на тело силе тяжести Fт только в том случае, если весы с телом относительно Земли покоятся или движутся равномерно и прямолинейно; В этом случае

Если же тело движется ускоренно, то его вес зависит от значения этого ускорения и от его направления относительно направления ускорения свободного падения.

Когда тело подвешено на пружинных весах, на него действуют две силы: сила тяжести Fт=mg и сила упругости Fyп пружины. Если при этом тело движется по вертикали вверх или вниз относительно направления ускорения свободного падения, значит векторная сумма сил Fт и Fуп дает равнодействующую, вызывающую ускорение тела, т. е.

Fт + Fуп=mа.

Согласно приведенному выше определению понятия "вес", можно написать, что Р=-Fyп. с учетом того, что Fт=mg, следует, что mg-mа=-Fyп. Следовательно, Р=m(g-а).

Силы Fт и Fуп направлены по одной вертикальной прямой. Поэтому если ускорение тела а направлено вниз (т.е. совпадает по направлению с ускорением свободного падения g), то по модулю

Если же ускорение тела направлено вверх (т. е. противоположно направлению ускорения свободного падения), то

Р = m = m(g+а).

Следовательно, вес тела, ускорение которого совпадает по направлению с ускорением свободного падения, меньше веса покоящегося тела, а вес тела, ускорение которого противоположно направлению ускорения свободного падения, больше веса покоящегося тела. Увеличение веса тела, вызванное его ускоренным движением, называют перегрузкой.

При свободном падении a=g. следует, что в таком случае Р=0, т. е. вес отсутствует. Следовательно, если тела движутся только под действием силы тяжести (т. е. свободно падают), они находятся в состоянии невесомости. Характерным признаком этого состояния является отсутствие у свободно падающих тел деформаций и внутренних напряжений, которые вызываются у покоящихся тел силой тяжести. Причина невесомости тел заключается в том, что сила тяжести сообщает свободно падающему телу и его опоре (или подвесу) одинаковые ускорения.

На поверхности Земли сила тяжести (гравитация ) постоянна и равна произведению массы падающего тела на ускорение свободного падения: F g = mg

Следует заметить, что ускорение свободного падения величина постоянная: g=9,8 м/с 2 , и направлена к центру Земли. Исходя из этого можно сказать, что тела с разной массой будут падать на Землю одинаково быстро. Как же так? Если бросить с одинаковой высоты кусочек ваты и кирпич, то последний проделает свой путь до земли быстрее. Не забывайте о сопротивлении воздуха! Для ваты оно будет существенным, поскольку ее плотность очень мала. В безвоздушном пространстве кирпич и вата упадут одновременно.

Шар движется по наклонной плоскости длиной 10 метров, угол наклона плоскости 30°. Какова будет скорость шара в конце плоскости?

На шар действует только сила тяжести F g , направленная вниз перпендикулярно к основанию плоскости. Под действием этой силы (составляющей, направленной вдоль поверхности плоскости) шар будет двигаться. Чему будет равна составляющая силы тяжести, действующей вдоль наклонной плоскости?

Для определения составляющей необходимо знать угол между вектором силы F g и наклонной плоскостью.

Определить угол довольно просто:

• сумма углов любого треугольника равна 180°;
• угол между вектором силы F g и основанием наклонной плоскости равен 90°;
• угол между наклонной плоскостью и ее основанием равен α

Исходя из вышесказанного, искомый угол будет равен: 180° - 90° - α = 90° - α

Из тригонометрии:

F g накл = F g ·cos(90°-α)

Sinα = cos(90°-α)

F g накл = F g ·sinα

Это действительно так:

• при α=90° (вертикальная плоскость) F g накл = F g
• при α=0° (горизонтальная плоскость) F g накл = 0

Определим ускорение шара из известной формулы:

F g ·sinα = m·a

A = F g ·sinα/m

A = m·g·sinα/m = g·sinα

Ускорение шара вдоль наклонной плоскости не зависит от массы шара, а только от угла наклона плоскости.

Определяем скорость шара в конце плоскости:

V 1 2 - V 0 2 = 2·a·s

(V 0 =0) - шар начинает движение с места

V 1 2 = √2·a·s

V = 2·g·sinα·S = √2·9,8·0,5·10 = √98 = 10 м/с

Обратите внимание на формулу! Скорость тела в конце наклонной плоскости будет зависеть только от угла наклона плоскости и ее длины.

В нашем случае скорость 10 м/с в конце плоскости будет иметь и бильярдный шар, и легковой автомобиль, и самосвал, и школьник на санках. Конечно же, трение мы не учитываем.

В. М. Зражевский

ЛАБОРАТОРНАЯ РАБОТА №

СКАТЫВАНИЕ ТВЕРДОГО ТЕЛА С НАКЛОННОЙ ПЛОСКОСТИ

Цель работы: Проверка закона сохранения механической энергии при скатывании твердого тела с наклонной плоскости.

Оборудование: наклонная плоскость, электронный секундомер, цилиндры разной массы.

Теоретические сведения

Пусть цилиндр радиуса R и массой m скатывается с наклонной плоскости, образующей угол α с горизонтом (рис. 1). На цилиндр действуют три силы: сила тяжести P = mg , сила нормального давления плоскости на цилиндр N и сила трения цилиндра о плоскость F тр. , лежащая в этой плоскости.

Цилиндр участвует одновременно в двух видах движения: поступательном движении центра масс O и вращательном движении относительно оси, проходящей через центр масс.

Так как цилиндр во время движения остается на плоскости, то ускорение центра масс в направлении нормали к наклонной плоскости равно нулю, следовательно

P ∙cosα − N = 0. (1)

Уравнение динамики поступательного движения вдоль наклонной плоскости определяется силой трения F тр. и составляющей силы тяжести вдоль наклонной плоскости mg ∙sinα:

ma = mg ∙sinα − F тр. , (2)

где a – ускорение центра тяжести цилиндра вдоль наклонной плоскости.

Уравнение динамики вращательного движения относительно оси, проходящей через центр масс имеет вид

I ε = F тр. R , (3)

где I – момент инерции, ε – угловое ускорение. Момент силы тяжести и относительно этой оси равен нулю.

Уравнения (2) и (3) справедливы всегда, вне зависимости от того, движется цилиндр по плоскости со скольжением или без скольжения. Но из этих уравнений нельзя определить три неизвестные величины: F тр. , a и ε, необходимо еще одно дополнительное условие.

Если сила трения имеет достаточную величину, то качение цилиндра по наклонной происходит без скольжения. Тогда точки на окружности цилиндра должны проходить ту же длину пути, что и центр масс цилиндра. В этом случае линейное ускорение a и угловое ускорение ε связаны соотношением

a = R ε. (4)

Из уравнения (4) ε = a /R . После подстановки в (3) получаем

. (5)

Заменив в (2) F тр. на (5), получаем

. (6)

Из последнего соотношения определяем линейное ускорение

. (7)

Из уравнений (5) и (7) можно вычислить силу трения:

. (8)

Сила трения зависит от угла наклона α, силы тяжести P = mg и от отношения I /mR 2 . Без силы трения качения не будет.

При качении без скольжения играет роль сила трения покоя. Сила трения при качении, как и сила трения покоя, имеет максимальное значение, равное μN . Тогда условия для качения без скольжения будут выполняться в том случае, если

F тр. ≤ μN . (9)

Учитывая (1) и (8), получим

, (10)

или, окончательно

. (11)

В общем случае момент инерции однородных симметричных тел вращения относительно оси, проходящей через центр масс, можно записать как

I = kmR 2 , (12)

где k = 0,5 для сплошного цилиндра (диска); k = 1 для полого тонкостенного цилиндра (обруча); k = 0,4 для сплошного шара.

После подстановки (12) в (11) получаем окончательный критерий скатывания твердого тела с наклонной плоскости без проскальзывания:

. (13)

Поскольку при качении твердого тела по твердой поверхности сила трения качения мала, то полная механическая энергия скатывающегося тела постоянна. В начальный момент времени, когда тело находится в верхней точке наклонной плоскости на высоте h , его полная механическая энергия равна потенциальной:

W п = mgh = mgs ∙sinα, (14)

где s – путь, пройденный центром масс.

Кинетическая энергия катящегося тела складывается из кинетической энергии поступательного движения центра масс со скоростью υ и вращательного движения со скоростью ω относительно оси, проходящей через центр масс:

. (15)

При качении без скольжения линейная и угловая скорости связаны соотношением

υ = R ω. (16)

Преобразуем выражение для кинетической энергии (15), подставив в него (16) и (12):

Движение по наклонной плоскости является равноускоренным:

. (18)

Преобразуем (18) с учетом (4):

. (19)

Решая совместно (17) и (19), получим окончательное выражение для кинетической энергии тела, катящегося по наклонной плоскости:

. (20)

Описание установки и метода измерений

Исследовать качение тела по наклонной плоскости можно с помощью узла «плоскость» и электронного секундомера СЭ1, входящих в состав модульного учебного комплекса МУК-М2.

У
становка представляет собой наклонную плоскость 1, которую с помощью винта 2 можно устанавливать под разными углами α к горизонту (рис. 2). Угол α измеряется с помощью шкалы 3. На плоскость может быть помещен цилиндр 4 массой m . Предусмотрено использование двух роликов разной массы. Ролики закрепляются в верхней точке наклонной плоскости с помощью электромагнита 5, управление которым осуществляется с помощью

электронного секундомера СЭ1. Пройденное цилиндром расстояние измеряется линейкой 6, закрепленной вдоль плоскости. Время скатывания цилиндра измеряется автоматически с помощью датчика 7, выключающего секундомер в момент касания роликом финишной точки.

Порядок выполнения работы

1. Ослабив винт 2 (рис. 2), установите плоскость под некоторым углом α к горизонту. Поместите ролик 4 на наклонную плоскость.

2. Переключите тумблер управления электромагнитами механического блока в положение «плоскость».

3. Переведите секундомер СЭ1 в положение режим 1.

4. Нажмите кнопку «Пуск» секундомера. Измерьте время скатывания.

5. Повторите опыт пять раз. Результаты измерений запишите в табл. 1.

6. Вычислите значение механической энергии до, и после скатывания. Сделайте вывод.

7. Повторите п. 1-6 для других углов наклона плоскости.

Таблица 1

	t i , c	(t i − <t >) 2	пути s , м	Угол наклона	ролика, кг	W п, Дж	W к, Дж
t (a,n )	<t >	å(t i – <t >) 2	Δs , м		Δm , кг

8. Повторите опыт п. 1-7 для второго ролика. Результаты запишите в табл. 2, аналогичную табл. 1.

9. Сделайте выводы по всем результатам работы.

Контрольные вопросы

1. Назовите виды сил в механике.

2. Объяснить физическую природу сил трения.

3. Что называется коэффициентом трения? Его размерность?

4. Какие факторы влияют на величину коэффициента трения покоя, скольжения, качения?

5. Описать общий характер движения твердого тела при качении.

6. Как направлен момент силы трения при качении по наклонной плоскости?

7. Записать систему уравнений динамики при качении цилиндра (шара) по наклонной плоскости.

8. Вывести формулу (13).

9. Вывести формулу (20).

10. Шар и цилиндр с одинаковыми массами m и равными радиусами R одновременно начинают скатываться по наклонной плоскости с высоты h . Одновременно ли они достигнут нижней точки (h = 0)?

11. Объяснить причину торможения катящегося тела.

Библиографический список

1. Савельев, И. В. Курс общей физики в 3­х т. Т. 1 / И. В. Савельев. – М.: Наука, 1989. – § 41–43.

2. Хайкин, С. Э. Физические основы механики / С. Э. Хайкин. – М: Наука, 1971. – § 97.

3. Трофимова Т. И. Курс физики / Т. И. Трофимова. – М: Высш. шк., 1990. – § 16–19.

Facebook

Twitter

Вконтакте

Одноклассники

Google+